HALLAMOS EL PERÍMETRO y el ÁREA

 

1º- OBSERVA BIEN LAS FIGURAS: 
-    ¿de qué figuras se trata?: ninguna es  una figura de las que hemos visto en clase. Por tanto, lo `primero será descomponer esas  figuras en otras más pequeñas que sí conozcas (cuadrados, rectángulos, triángulos, trapecios, rombos, círculos).
-    Fíjate en la unidad que vienen los datos. En la figura a) vienen todos en mm   (milímetros). En la figura b) vienen mezclados, hay datos en cm (centímetros), en m(metros), dm (decímetros) y mm (milímetros).
En los dos casos será necesario pasar todas las unidades a la misma unidad y después operar con ella.  Por tanto habrá que recordar cómo pasar de una unidad a otra (medida de longitud)


¿QUÉ PIDE EL EJERCICIO?:  Te piden que halles el perímetro de cada figura.
La figura a) hay que expresarla en  decímetros (dm) y vemos que los datos vienen marcados en mm (milímetros). Podemos pasar todos los datos a dm y luego operar o primero podemos operar, obtener el resultado en mm y después pasarlo a dm, tal y como exige el  ejercicio.
En el ejercicio a) observamos tres figuras: un rectángulo, un cuadrado y un triángulo.   El perímetro es la suma de todos los lados. Comprueba si conoces todos los lados.  Lo más práctico es completar todos los datos que faltan:












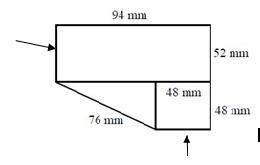
El perímetro sería, comenzando por arriba y hacia la  derecha:
94 + 52 + 48 + 48+ 76+  52 = 370 mm
Como nos piden en dm, la solución al ejercicio sería : 370mm= 3,70 dm


En la figura B optamos por  pasar todas las unidades que tiene la figura a la que nos piden, a metros. 

Por tanto la figura quedaría así:

Por tanto el Perímetros sería (comenzando por la línea superior y hacia la derecha):
0,134 + 0,062 + 0,062 + 0,06 + 0,03+ 0,06 + 0, 068 =  0,476 metros.

VAMOS A POR LAS ÁREAS

La primera figura se descompone en tres figuras conocidas:

Ahora aplicamos  las fórmulas de cada figura, para después sumarlas y hallar el área total.

ÁREA DEL RECTÁNGULO=  b . a =  94 . 52 =
ÁREA DEL TRIÁNGULO=  b. a   =  la base es 48 mm y la altura  94 menos 48 mm.
                                                  2
ÁREA DEL CUADRADO:  l . l =  48 . 48 =

La suma de todas las áreas dará como resultado el área total.

Figura 2:  Está formada por varias figuras: triángulos y  rectángulos.  Debes tener en cuenta que hay que operar en la misma unidad (utilizando por ejemplo los datos del ejercicio anterior).

Tenemos un tríangulo de color rojo. A= b.a   =
                                                                   2
Otros dos  triángulos  de color amarillo y gris , iguales. A= b.a =
                                                                                                 2
Un rectángulo verde.  A=  b. a=

Y un rectángulo pequeño, de color azul. A= b. a =

                                    ¿Cuál es la solución al ejercicio? ¿Qué área no podemos hallar porque nos faltan datos?  ¿Se pueden hallar los datos que faltan con lo que sabemos?