SOLUCIONES

Para corregir el cuadernillo de problemas que lleváis de deberes (uno de los grupos, el resto , las tenéis en la última hoja del cuaderno) , aquí tenéis las primeras soluciones.



1.-S: 6 cajas.
2.- S: 20 semanas.
3.-S: A Rafael 60 € y a Marisa 80 €.
4.- S: 18.000 litros de agua.
5.- S: 75 cajas.
6.- S: Pesa la carga : 5.200 kg.
Vale la carga: 37.200 €.
7.- S: 2.108 €
8.- S: 1.380 €
9.- S: 223 huevos.
10.- S: 46.189 planchas
11-S- 1056 botellas
12- S-17 euros
13-S- 74 kg
14- S-96000 folios
15- S-306 euros
16-
17-S- 3744 pasteles
18-S-32.895 alevines
19- S-29,20 euros
20- S- 948
21-S- 221.235
22-S-13,5
23-S- 37,82
24-S-29
25-S-684
26-S-650
27-S-8
28-S-10
29-S-112
30- S-108
31-S-11,6
32-S-1,20
33-S-7,2
34-S-1,55
35-S-8
36-S-7
37-S-5
38-S-3,2
39-S-
40-S

problemas, control diciembre

1- Adriano tenía ahorrados 200 euros y ha gastado 50 euros en un reproductor de MP3. ¿Qué % de sus ahorros ha gastado?

2- Un paquete de 500 folios pesa 1,8 kg. ¿cuánto pesará una pila de 850 folios?

3- Un granjero necesita cada día 255 kg de pienso para dar de comer a sus 85 vacas. ¿Cuántos kilos necestaría si vendiera 35 vacas?

4- Dos trabajadores recolectan la uva de una viña en 9 horas. ¿Cuánto tardarían en hacer lo mismo 3 trabajadores?

5- Por el alquiler de una bicicleta durante dos horas pago 3 euros. ¿Cuánto pagaré si la alquilo durante siete horas?

6- Un jugador de baloncesto ha efectuado 25 lanzamientos y ha conseguido 16 canastas. ¿Cuál es su porcentaje de aciertos?

7-Una merluza de dos kilos y trescientos gramos, ha costado 28,75 euros. ¿Cuánto pagaré por otra más pequeña de kilo y medio?

8- Un ciclista a 20 km/h tarda 30 minutos en cubrir cierto recorrido. ¿cuánto tardará una moto a 60 km/h?

9- En una clase de 30 alumnos, el 80% votaron a María, la actual delegada y el resto a Eduardo. ¿Cuántos votos recibió Eduardo?

proporciones, control 29 noviembre

Aquí tienes las preguntas del ejercicio de clase del 29 de noviembre. Puedes colaborar en su resolución en este enlace.


1- El 25% de los 600 litros de leche que producen al día, lo destinan a la fabricación de queso. ¿Cuántos litros son?

2- Entre estos pares de magnitudes, di cuáles guardan relación de proporcionalidad (si es Directa pon D y si es Inversa por I) o no guardan ninguna relación.
a) la edad de un árbol y su altura:
b) la cantidad de agua que arroja una fuente y el tiempo que transcurre
c) el caudal de un grifo y el tiempo que tarda en llenar un cántaro.
d) el coste de un bolígrafo y el tiempo que dura.
e) la velocidad de un vehículo y la distancia recorrida en media hora.
f) el número de páginas de un libro y su precio.
g) el número de kilos vendidos y el dinero recaudado.


3- ¿Cuánto pagaré por 300 gramos de salmón ahumado que cuesta 16 euros el kilo?


4- Un tractor ara un campo en 15 horas.
a) lee las preguntas  c, d y e y dí si es una proporción Directa o Inversa
b) construye la tabla de proporcionalidad
c) ¿Cuánto tardarán dos tractores?
d) ¿y tres tractores?
e) ¿y cuatro tractores?


5- En clase somos 30 y el 90% hemos aprobado el examen de matemáticas. ¿cuántos han suspendido?


6- Alberto ha comprado un abrigo que costaba 148 euros pero le han hecho una rebaja del 25 %. ¿Cuánto ha pagado por el abrigo?


7- Halla el m.c.m. (15, 18, 24)


8- Ana ha pagado 60 euros por alquilar una furgoneta durante 2 días. ¿Cuánto le cobrarán por alquilarla 5 días?

9- Explica qué son números primos y escribe los primeros 20.

múltiplos

Hoy hemos dado en clase cómo hallar el MÍNIMO COMÚN MÚLTIPLO.

Ejemplo:   Nos piden hallar esta operación.

20 ,  +  12,   +   4
24        36         40

1º  Tenemos que hallar el DENOMINADOR COMÚN con el nuevo método de DESCOMPONER LOS NÚMEROS EN FACTORES PRIMOS

Números Primos son aquellos que solo tienen como DIVISORES a ellos mismos y al 1.  Es decir, que los números primos son el 1, 2, 3, 5, 7, 11, 13, 17, 19, 23...

Así sería la descomposición: RECUERDA , a la derecha  de la barra SOLO pueden aparecer NÚMEROS PRIMOS.

Ahora escribimos esos factores primos en forma de POTENCIAS,  

Y tenemos que fijarnos:

- el número 2 es un factor común a los tres números.  

- los números 3 y 5 son factores NO comunes, pues no están en todos.

elegimos: 

- los FACTORES COMUNES CON MAYOR EXPONENTE

- los factores NO COMUNES,  cogemos TODOS.

2º Ahora ya sabemos cuál es el m.c.m  :    8 .  9 .  5  que es igual a 36o.

3º  Ya podemos sumar con el procedimiento habitual:

20 ,  +  12,   +   4
24        36         40

______  +________ +________

360              360             360

15. 20    +    10. 12    +    9. 4   

 360                360            360 

  

problemas 16 de noviembre

EJERCICIO 1

A.Se dice que pasamos un tercio de nuestra vida durmiendo. Si vivimos 81 años, ¿cuánto tiempo habremos  estado durmiendo?

B.En una clase de 36 alumnos  1/3  han elegido como optativa el idioma francés y  1/6  el alemán. ¿Qué fracción de alumnos estudian idiomas? ¿Cuántos son?

EJERCICIO 2

A. Pedro se ha gastado los 3/5   de su paga. ¿Cuál es su paga si se ha gastado 24 euros?

B. Los alumnos de Primero van a visitar una reserva de animales. Se sabe que van los  ¾  y se quedan 36. ¿Cuántos alumnos hay en 1º?

EJERCICIO 3

A.Dos hermanos están leyendo el mismo libro.  Luis lleva leído 2/5 del libro y  José  3/7.  ¿A quién le falta más páginas por leer

B. Por la mañana he pintado 3/5 de la valla. Por la tarde,  la mitad de lo que quedaba. ¿Qué fracción de valla me queda por pintar?

EJERCICIO 4

A. Un balón cuesta  30 €. ¿Cuánto pagaremos por él si nos descuentan el 15%?

B.Una persona pagaba el año pasado por el alquiler de su vivienda 420 € mensuales. Este año le han subido el precio un 5%. ¿Qué mensualidad tendrá que pagar ahora?

EJERCICIO 5

D. Para hacer dos tartas de manzana, Ricardo ha empleado 12 manzanas. ¿Cuántas manzanas necesitará para hacer 9 tartas?

D. Dos calcetines puestos a secar en un radiador tardan 3 horas en secarse. ¿cuánto tardarán en secarse 5 calcetines?

EJERCICIO 6

C. Un balón que cuesta 8 € nos lo han vendido por 6,8 €. ¿Qué tanto por ciento de descuento nos han hecho?

SIGUE ESTE ENLACE PARA COLABORAR EN SOLUCIONARLOS O PARA CORREGIRLOS.

fracciones, ejercicio 9 de noviembre

1- Juan ha  ido a comprar un juego para su playstation con los 25 euros que le ha dado su madre. Cuando ha llegado a la tienda se ha encontrado con que habían subido todos los juegos un 10%. ¿cuánto dinero le falta? ¿cuánto cuesta ahora el juego que Juan quería comprar?

8-     ¿Cuántas botellas de ¾  de litro se pueden llenar con una garrafa de 30 litros?

2   5-Pepe sale de su casa con 30 euros . Se gasta 2/5 del dinero en un libro y después 4/9 de lo que le queda en un disco. ¿Con cuánto dinero vuelve a casa?

3  2-Pepe, Luis y  María han recibido una caja de bombones cada uno. Pepe se ha comido 5/7 de los bombones de su caja; Luis  2/5 de los bombones de la suya y María  7/12. ¿A cuál de los tres le quedan más bombones en su caja?

47- He gastado ¾ partes del dinero que tenía y me quedan 800 euros.  ¿cuánto  tenía?

54- Por 3 horas de trabajo,  Juan cobra 60 euros. ¿cuánto cobrará por 8 horas de trabajo?

¿ 3-   ¿Cual será el precio de un móvil que cuesta 250 euros si tiene un 25% de descuento?

7 6- Tengo ahorrado 500 euros y quiero ponerlos en un depósito durante un año. ¿qué oferta será mejor?

a.       Banco Santander:  3 % los 6 primeros meses y 2 % el resto.

b.      ING :  4% los 3 primeros meses y 2%  el resto.



ENLACE PARA  CONTRIBUIR  A SOLUCIONARLOS

más fracciones (control 5 noviembre)

11-      Cuántos litros caben en ocho botellas de tres cuartos de litro?

22-      En el hundimiento del  Titanic murieron 1.500 personas, que suponían 10/12 del pasaje. ¿Cuántas  personas viajaban en el barco?

44-      ¿Cuánto costará un televisor cuyo precio era 789 euros si me hacen un 20% de descuento?

55-      De los 650 alumnos del colegio, 3/5 son chicas. ¿cuántos chicos hay?

66-      Un librero ha comprado 80 libros. Vende los 5/8 a 10,50 euros cada uno y el resto a 12 euros cada uno. Obtiene una ganancia de 305,80 euros. ¿Cuánto le habían costado los libros?


eENLACE PARA LAS SOLUCIONES


s

PORCENTAJES

Vamos a avanzar un poco en este tema de las fracciones.  Los porcentajes no dejan de ser eso, fracciones.  Fíjate en estos ejercicios.    EJERCICIOS

Después de entenderlo bien y practicar un poco en clase,  seguiremos haciendo ejercicios.

CONTROL DE MATES: 26-O . FRACCIONES II

Este es el ejercicio que hemos tenido que realizar hoy para terminar el tema de las fracciones. Ya está abierta la página para poner/ver las soluciones (enlace al final):

1-    Esther y su abuelo beben ¾ de litro de leche al día cada uno. ¿Qué cantidad de leche beben entre los dos en una semana?

2-    En  un jardín se han plantado 322 árboles. Si  3/7 son castaños, ½ son pinos y el resto chopos, ¿cuántos árboles hay de cada tipo?

3-    En una clase, 4/7 de los alumnos practican natación y 3/10 waterpolo y el resto no hace ningún deporte. ¿Qué fracción de la clase practica  estos deportes?  ¿qué fracción no practica ningún deporte?

4-    Quiero comprar una televisión que cuesta 400 euros.  Si me hacen un 30% de descuento. ¿Cuánto me costará la televisión?

5-    Dos hermanos se reparten las canicas de un bote. El primero se lleva

3/8 del total, mientras que el segundo obtiene las 55 restantes. ¿Cuántas contenía el bote?

6-    Los libros de 1º de la ESO costaban el año pasado  300 euros y tenían incluido un 8% de IVA.  Como ha subido el IVA del 8% al 21%,  ¿cuánto costarían esos libros este curso?

7-    Operaciones rápidas

a.     Halla los 2/3 de  150

b.     2/5 +  3/5=

c.      3/4  .  2/7 =

d.     5/6 :  1/3 =

e.     3/4 -  2/5 =

¿son equivalentes  a 1/3?    2/6      4/12    16/ 48      7 /24     24/72     

Simplifica hasta hallar la fracción irreducible:

420/126= 

Como siempre,  podemos ayudar entre todos a explicar los problemas en ESTE ENLACE.
Una vez que esté el control bien hecho y corregido, se cerrará la página y no se podrá escribir, sólo se podrá ver.

Control de fracciones 19-O

1-La asociación El Refugio ha recogido 150 animales abandonados. Dos quintos son gatos y el resto, perros.
¿Cuántos gatos han recogido? ¿Y perros?


2- El ciclista ha recorrido los 2/3 de la etapa. ¿Qué distancia ha recorrido? ¿Cuánto le queda para llegar a la meta?


SALIDA----------------(150 KM)------------------META



3- Calcula los 3/5 del dinero que tiene Rocío.    (tiene dos billetes: uno de 5 euros y otro de 10)



4- Una sesión de circo consta de dos tiempos de 3/4 de hora cada uno, separados por un descanso de un cuarto de hora. Calcula la duración total de la sesión.


5- Carlos compró cinco bolsas de fresas. ¿Cuántos kilos compró? (cada bolsa tiene 3/4 Kg).

6- Un balón cuesta 300 euros. Me rebajan un 15%.  ¿Cúánto pagaré?


7- Un ordenador está rebajado un 35%. Si su precio era de 1.200 euros. ¿Cuánto será su precio final?



 SOLUCIONES PARA CORREGIR

PROBLEMAS DE FRACCIONES

Aquí tenéis los problemas de mates.  El día de entrega es el Jueves próximo.
Si tenéis dudas en fracciones (además de preguntar en clase, claro) podéis visitar alguna de los enlaces que encontraréis a la derecha con la ETIQUETA FRACCIONES.  Hay muchas páginas  con teoría y ejercicios, muchos de ellos interactivos, con los que vosotros mismos podréis saber si acertáis o no y qué errores cometéis.

PÁGINA 107

4- Gonzalo ha comprado una botella de aceite de tres cuartos de litro y otra de litro. ¿Cuántos cuartos de litro lleva en la bolsa?
5- En el cumpleaños de Hortensia se consumieron siete décimas partes de la tarta. ¿Qué fracción de tarta queda?
6- Mi madre hizo dos pizzas y nos comimos 11/8 de pizza. ¿Qué fracción de pizza queda?


PÁGINA 109

6- Marta ha bebido un tercio de litro de leche en el desayuno y un cuarto de litro en la cena. ¿Qué cantidad de leche ha bebido en el día?
7- Julio ha sembrado la mitad de su huerta de lechugas y la quinta parte de tomates. ¿Qué fracción de la huerta ocupan ambas hortalizas?
8- Con una botella de litro lleno, tres cazos o cuatro vasos?. ¿Cuál es al diferencia de capacidad entre un cazo y un vaso?  (recuerda ayudarte de un dibujo)

PÁGINA 111.

6- Raúl y dos amigos han merendado en la pizzería. Cada uno ha tomado 3/5 de pizza. ¿Qué cantidad de pizza han tomado en total?
7- Una caja de refrescos contiene 20 botellas de 2/5 de litro cada una. ¿Cuántos litros de refresco hay en la caja?

PÁGINA 113
7- Ayer, Leonor nos trajo media tarta, que repartimos entre los cuatro que somos en casa. ¿Qué fracción de tarta nos tocó a cada uno?
8- Una botella de aceite de tres cuartos de litro ha durado en mi casa 6 días. ¿Qué fracción de litro consumimos cada día?
9-¿cuántos lazos puedo hacer con metro y medio de cinta, si cada lazo necesita un octavo de metro?

PÁGINA 115
12- Clara gasta la mitad de su dinero en unos zapatos y la quinta parte en una blusa. ¿Qué fracción de dinero ha gastado?
13- Berta, Andrés y Marga compran un regalo para su madre. Berta pone la quinta parte del dinero. Andrés, los tres décimos y  Marga, el resto. ¿Qué fracción de dinero pone Marga?
14- ¿Cuántos litros de refresco contienen 30 botes, sabiendo que cada bote lleva un tercio de litro?
15- ¿Cuántas botellas de tres cuartos de litro  se llenan con una garrafa de aceite de 30 litros?


Cuando terminéis cada página podéis comprobar las soluciones  AQUÍ    (claro, antes alguno de vosotros debe poner las soluciones).

20.000 VISITAS

Termina el curso y llega el verano, tiempo para descansar y prepararse para un nuevo curso.  Y lo hacemos con 20.000 visitas en nuestra web.

En febrero de 2010 nos alegrábamos por llegar a las 5.000 visitas.  En poco más de dos años  hemos  multiplicado por 4 esa cifra. Eso significa que esto funciona.  ¡Enhorabuena a todos!

FÚTBOL Y MATEMATICAS

Leo en el periódico que cada jugador de la Selección Española  cobrará 300.000 euros si ganan la Eurocopa.
 

Esto nos servirá para hacer algunos problemas matemáticos pero antes necesitaremos algunos datos para echar cuentas:

número de jugadores de la seleccón:_______
número de entrenadores, médicos, ayudantes... (equipo técnico al completo):_________
número de partidos que jugará la selección si llega a la final:____________
AQUÍ puedes encontrar alguna información

Teniendo en cuenta esos datos,  hay que contestar a las siguientes cuestiones:

1-  ¿Cuánto es el total de dinero que nos costará  la prima a la Selección por ganar?_________________

2-  ¿Cuánto tiempo (en años) tendría que trabajar un  empleado que cobrara 1.200 euros al mes para ganar lo que ganarán cada uno de los seleccionados?

3- ¿A cómo sale el partido de la Eurocopa para un jugador?

4- ¿A cómo sale el minuto de juego?

5-  Si con el total del dinero se quisiera dar una ayuda de 500 euros a las familias durante un año. ¿Cuántas familias podrían beneficiarse?


Por cierto, que tendríamos que estar contentos con la noticia porque en la anterior Eurocopa, en Austria, cada jugador se llevó 500.000 euros enteritos y por el Mundial 600.000 euros. No está mal. Pero mejor no echar más cuentas, no sea que además caigamos en la cuenta de otras cosas... y empecemos a pensar.

MATEMÁTICAS EN LA VIDA

Seguimos con nuestras entradas sobre la utilidad de las matemáticas.  En este vídeo veremos cómo están muy relacionadas con las Ciencias Naturales.

MATEMÁTICAS EN LA VIDA

Hoy Dani nos preguntaba que para qué servían las matemáticas, todo el día liándonos con fracciones, ecuaciones, geometría,  números negativos.... y ¿para qué? ¿nos van a servir - se preguntaba Dani- para algo en la vida?

Así que vamos a comenzar algunas entradas sobre la utilidad de las matemáticas y seguro que vosotros, si pensáis un poco, dais con la solución, o ,al menos, con algunas soluciones.

Empezaremos viendo este vídeo, realizado por unos estudiantes (está en catalán pero se entiende perfectamente) para ver que a nuestro alrededor las mates  "nos acechan" por todos lados.

Un genio matemático con 16 años

Shouryya Ray es el nombre de un chico de 16 años que ha 


protagonizado una noticia alucinante. Ha resuelto un problema propuesto por 


Newton hace más de 350 años. Muchos matemáticos a lo largo de este tiempo intentaron resolver el dilema pero no lo consiguieron.




Es un chico indio, nacido en Calcuta, pero llegó a Alemania con 12 años para estudiar.   Según la noticia 
Ha sabido resolver dos problemas relacionados con la dinámica de partículas para los que hasta ahora solamente se podían encontrar soluciones aproximadas con la ayuda de ordenadores. Son calcular la trayectoria exacta de un proyectil afectado por la gravedad y por la resistencia del aire (el propuesto por Newton hace más de 300 años) y predecir cómo golpeará y rebotará en una pared.

Lo curioso es que lo hizo como un trabajo escolar en un concurso de mates y ...¡quedó en segundo lugar!  Según ha declarado, no se siente como un genio porque dice que todo es fruto de la "curiosidad".

RESULTADOS DEL CONCURSO SUPERT MATIK

Esta tarde se ha publicado los resultados del Campeonato de Cálculo Mental SUPER-T MATIK.  
Nuestros compañeros, Olayo Quiñonero y Noel Jiménez , representaban a nuestro colegio en la FASE FINAL ON LINE.

               ¡¡ FELICIDADES !!


Noel ha logrado el puesto 50 y  Olayo el 344 
                       de un total de ....


212.000 participantes de 52 nacionalidades




Ellos han contribuido a que España se coloque en el 2º puesto en la clasificación por países,  solo superada por el país anfitrión y organizador, Portugal (en la imagen puedes ver los primeros veinte países clasificados)

concurso Super T matik

Esta semana nuestros compañeros Olayo y Noel, las mentes más rápidas en esto de los números,  van a participar en la FINAL  del Concurso Super T Matik representando al Colegio Ventura Rodríguez.

¡Suerte!   ¡Seguro que lo hacéis muy bien!

EXAMEN DE 6º

El próximo día 9 de mayo tendrás que realizar la Prueba de Conocimientos y Destrezas Indispensables (CDI) que organiza la Comunidad de Madrid

En esta página tienes todas las pruebas desde 2005.

ESTADISTICA

Hemos empezado los últimos temas de matemáticas.

Con las notas de las "quinielas" de Cono ya hemos aprendido a  construir una TABLA DE FRECUENCIAS y  a  calcular la media aritmética.  También a buscar el dato con ese nombre tan raro:  la MODA

La frecuencia absoluta es el número de veces que se repite un dato.
La moda es el dato que tiene mayor frecuencia absoluta (es decir, el dato que se repite mayor número de veces)

TEORÍA  (EDITORIAL ANAYA)


TABLAS Y GRÁFICOS ESTADÍSTICOS

DIVISORES

LOS DIVISORES DE UN NÚMERO

 Otras páginas:

PARA REPASAR TEORÍA Y HACER ALGUNOS EJERCICIOS SENCILLOS

EJERCICIOS DE 6º DE LA EDITORIAL ANAYA

Si tienes dudas puedes utilizar esta "calculadora" que te "sopla"  los divisores de un número (pero recuerda que lo importante es entenderlo y saber hacerlo tú solito/a, porque el día del examen .... no tendrás ayuditas).

NUESTRAS TABLAS DE MULTIPLICAR

Nunca es tarde para repasar las tablas.  ¡ Vamos allá!:

TABLA DEL DOS:  Alex, Alicia, Marius y Santi.

dos por uno es dos,  tengo tos

dos por dos cuatro, vuelvo en un rato

dos por tres seis, ahora no me veis

dos por cuatro ocho, voy a llamar a los pelochos

dos por cinco diez, me como una nuez

dos por seis doce, tu tía se llama Conce

dos por siete catorce,

dos por ocho dieciseis, me visto de beis

dos por nueve dieciocho, quiero ser pinocho

dos por diez veinte, ¡uy! el niño no miente

TABLA DEL TRES :   Paula Maza, Ari,  Solange y Daniel

tres por uno tres, el mundo al revés

tres por dos seis, ¿vosotros lo véis?

tres por tres nueve, mañana llueve

tres por cuatro doce, ni me roces

tres por cinco quince, se extingue el lince

tres por seis dieciocho, me compré un poncho

tres por siete veintiuno, sale la luna

tres por ocho veinticuatro, ayer fui al teatro

tres por nueve veintisiete, terminamos en un periquete

tres por diez treinta, ¡se acabó la cuenta!

TABLA DEL CUATRO: Romina, Sorin, Dulce y Judith

cuatro por uno cuatro, eso es lo que hago todo el rato

cuatro por dos ocho, eso está pocho

cuatro por tres doce, me gusta que él goce

cuatro por cuatro dieciséis, no os beséis

cuatro por cinco veinte, ayer vi a Vicente

cuatro por seis veinticuatro, nos vamos al teatro

cuatro por siete veintiocho, me ofrecieron un bizcocho

cuatro por ocho, treinta y dosdos, ese burro me ha dado una coz

cuatro por nueve treinta y séis , ¿cómo lo véis?

cuatro por diez cuarenta, yo soy de los 80.

TABLA DEL CINCO:   Paula Martínez,

¡ Érase una vez una tabla al revés! :

cinco por diez cincuenta, ya hemos perdido la cuenta

cinco por nueve, cuarenta y cinco, corro, chuto y brinco

cinco por ocho,  cuarenta, siempre echo la cuenta

cinco por siete treinta y cinco, tengo un ornitorrinco

cinco por seis, treinta, me gustan los chicles de menta

cinco por cinco, veinticinco, dibujo, pinto y pinto

cinco por cuatro, veinte, le duele la frente

cinco por tres quince, corre como  un lince

cinco por dos diez, en mi  cole tengo un pez

cinco por uno cinco,  ¿lo echan por Telecinco?

TABLA DEL SEIS: Andrea, Rubén, Olayo y Samuel

seis por una es seis,  por la noche no me véis

seis por dos doce, es carroza y no "carroce"

seis por tres dieciocho,  tu derrochas, yo derrocho

seis por cuatro veinticuatro, hay un gato en el teatro

seis por cinco  treinta, mi cabeza ya da vueltas

seis por seis treinta y seis, míralo y ya veríes

seis por siete cuarenta y dos, mi saludo va por vos

seis por ocho, cuarenta y ocho, la nariz de Pinocho

seis por nueve, cincuenta y cuatro, no intrepreto en el teatro

seis por diez, sesenta, ¡terminamos la cuenta!


TABLA DELSIETE : Noel

siete por uno siete, me invitaron a un guateque

siete por dos catorce

siete por tres veintiuno, me tomo el desayuno

siete por cuatro veintiocho, ayer bebí calimocho

siete por cinco, treinta y cinco, pego  un salto y doy un brinco

siete por seis, cuarenta y dos, es la una y ventidos

siete por siete, cuarenta y nueve, ¡me encanta la nieve!

siete por ocho,  cincuenta y seis, yo aquí contando mientras coméis

siete por nueve, sesenta y tres, te huelen los piés

siete por diez setenta, ella está atenta.

21 DE MARZO DÍA MUNDIAL DE LA POESÍA

No, no nos hemos equivocado.  Este es nuestro blog de Mates. Os estaréis preguntado a qué cuento viene esta entrada sobre la poesía en un blog de cuentas y números.   Hoy hemos pasado el día recitando y componiendo poemas y , la verdad, es que para algunos ha sido un "problema" porque no  le "salían las cuentas".  ¿eso no son mates?
Es una broma pero claro que hay poesías matemáticas. Lee esta

Porque no faltan beli.....3      (belitre significa pícaro, ruín)

que a estafar acostumbra..2

hacen con estos cuita.....2    (cuitados significa tímido, desgraciado)

el oficio de los bui......3

¡Cuántos chalecos fia.....2

y pantalones medi.........2

que luego han sido pedi...2

y nunca han sido paga.....2!

Es dura verdad, no arras..3

a decir que en ambos mun..2

hierven rencores profun...2

en contra de nuestros sas.3

Vienen a nuestros merca...2

baratísimos vesti.........2

por los franceses vendi...2

y por nosotros compra.....2

                                            (Anónimo)

 Ahora vamos a crear nuestras propias poesías, utilizando las tablas de multiplicar. En unos días las pondremos aquí. ¡A ver que nos sale!

ESTADISTICAS DE LENGUAWEB

Nuestra "Lenguaweb" alcanza las 17.000 visitas.  La mayoría, lógicamente, proceden de España pero tenemos algunas visitas de muchos países del mundo. ¡Que guay que lo que nosotros escribamos lo lean en Argentina, en México, en Perú, o en Estados Unidos, Suecia o Alemania !
Aquí podemos ver las estadísticas del día 9 de marzo de 2012.

29 de Febrero

¿Conoces a alguien que halla nacido el 29 de Febrero? ¿Quizá tú mismo?
¿Que por qué te preguntamos eso? Pues porque si has nacido un 29 de febrero, hoy es tu cumpleaños. ¡FELICIDADES!
Y porque nos parece algo curioso.
No me digas que no es curioso que sólo puedas celebrar tu cumpleaños ¡UNA VEZ CADA CUATRO AÑOS! ¿Y los regalos? Bueno, lo mejor sería celebrar el cumple otro día como hacemos los niños, el viernes de esa semana, caiga en lo que caiga y así te aseguras que te regalan algo y que soplas las velas de la tarta.

2012 es un AÑO BISIESTO. Es decir, que tendrá 366 días y no 365 como cualquier año "normal". Esta es la explicación:

Porque la Tierra gira sobre sí misma 365.242375 veces al año pero un año normal tiene 365 días, así que hay que hacer algo para "alcanzar" esos 0.242375 días al año.
Así que cada cuatro años tenemos un día extra (el 29 de febrero), lo que hacen 365.25 días al año. Esto es bastante exacto, pero habrá 1 día de diferencia cada 100 años.
Así que cada 100 años no tenemos año bisiesto, y eso da 365.24 días al año (1 día menos cada 100 años = -0.01 días al año).
¡Todavía no es lo suficientemente exacto! Así que otra regla es que cada 400 años hay un año bisiesto. Con esto son 365.2425 días al año (1 dia recuperado cada 400 años = 0.0025 días al año), lo que está bastante cerca de 365.242375 como para que no importe mucho.

MAS INFORMACIÓN SOBRE LOS AÑOS BISIESTOS

LLÁMALE X

Cuando algo no se conoce o no se recuerda bien, se suele decir: "Llámalo x".

El Álgebra es la parte de las Matemáticas que estudia la relación entre números, letras y signos. Pues el Álgebra  que estudiamos consiste en hacer operaciones con cantidades desconocidas con las cuales operamos como si conociéramos su valor.

Un matemático, astrónomo y poeta árabe, Omar al-Khayyam (1048-1131) se dedicó a la resolución de ecuaciones y escribió un libro muy importante sobre el tema.

Para representar a la incógnita utilizaba el término áraba "shay" que significa "cosa". Esa y otras palabras fueron traducidas en España en esa época y al hacerlo se escribió como "xay". Poco a poco, para abreviar se fue reemplazando por su primera letra inicial, la x.

Así se convirtió en el símbolo universal de la incógnita en todas las ecuaciones y en la pesadilla de muchos estudiantes , ¿a que sí?

ECUACIONES

Desde muy pequeño ya sabes hacer ecuaciones. Es una de las  primeras lecciones  que aprendemos en el colegio. Mira estos ejercicios:


___ + 6 = 8




19 - ____ =   8




5 x ____ =   25


¿qué número sumado a 5 da como resultado 9?

¿ Por  qué número hay que dividir a 27 para obtener como resultado  9?
¿Has tenido problemas para resolverlos?  Seguro que no. Son ejercicios que resolvías ya en 3º de Primaria. Bueno,pues ya sabes resolver ecuaciones.  Ahora toca profundizar y aprender más para enfrentarnos a los que "verás" el año que viene en el Instituto.



Una ECUACIÓN  es una igualdad que se cumple para algún valor de la incógnita.

x + 5 = 7 (se cumple para el valor de x =2)

Una ecuación tiene dos miembros, cada uno a un lado del igual.     x + 5 ( 1º miembro)   =   7 (2º miembro)

Los números se llaman términos   (x + 5 =  7)   y  la letra que aparece, incógnita.   x + 5 = 7

La solución es el valor que le damos a la incógnita para que se cumpla la igualdad. x = 2


DESPEJAR la incógnita es conseguir aislar la X a uno de los lados de la igualdad y hacerle corresponder el valor numérico que quede al otro lado.

Para despejar la X de una ecuación seguiremos los siguientes pasos:

1º- colocar todos los términos con X a la izquierda del igual
2º- colocar todos los términos sin X a la derecha del igual.
3º- operar cada uno de los miembros
4º- despejar la X y hallar la solución.

Cuando un término pasa de un miembro al otro lo HACE CON LA OPERACIÓN CONTRARIA.

Veamos por qué:
La primera norma para las ecuaciones es que si se opera en un miembro hay que realizar LA MISMA OPERACIÓN en el segundo miembro PARA QUE SE MANTENGA LA IGUALDAD.
 Por ejemplo:
 4 +  10 =     14
Si sumo por ejemplo 5 al primer miembro, tengo que sumar 5 también en el segundo para que se mantenga la igualdad y sea cierto que se cumple.
4 + 10 + 5 =  14 + 5;   

Veamos qué supone eso en la práctica:

x + 7 =   12.
Para eliminar el 7 tengo que restarle 7 (en los dos miembros)
x + 7 -7 =  12- 7
Si continúo operando, como siete menos siete es cero:

x=  12- 7 ;   x =  5. 

En definitiva,  el  + 7  que estaba en el primer miembro de la primera operación   ( x + 7 = 12) , se ha convertido en - 7  en el desarrollo.

Por eso en clase escuchas esto:

x + 7 = 12.

Despejo la x /  Dejo el 12 sin hacerle nada puesto que sigue en el segundo miembro y "me llevo" el 7. Como el 7 está sumando en el primer miembro, me lo llevo al segundo miembro restando.

X= 12 - 7.      ;   X= 5.

Seguro que cuando hagas muchas ecuaciones lo encontrarás más fácil.  Esto es como  tantas y tantas cosas que son sencillas de hacer pero dificil de explicar (¿te suena, verdad, eso de. "me lo sé pero no sé cómo explicarlo").

Pondremos muchas ecuaciones y su solución para que practiques en casa. Comienza por estas (las soluciones puedes ponerlas en los comentarios y las corregimos en seguida). Pero NO DEJES DE PREGUNTAR LAS DUDAS EN CLASE.

3 + x =  8                 

5.x =  40

8x + 3 = 5x + 42



Ecuaciones resueltas

x + 8 =  12.  
X=  12 - 8   Despejamos la X.  Dejamos el 12 y nos llevamos el 8 (cambiamos el +8 por -8)
x = 4.    
Como puedes ver cada igualdad va en una línea distinta. No ponemos "dos iguales"  en una misma línea. Asi conseguiremos mayor claridad en la resolución de los ejercicios y evitaremos confusiones.

6x = 48;       
 x=  48 / 6     Despejamos la X.  Dejamos el 48 y nos llevamos al segundo miembro el 6 que antes
                     multiplicaba y ahora divide.
 x= 8.  


2x- 7 = x + 17 
2x  - x =  17 + 7  
X = 24
1º pasamos las X a la izquierda del igual, y  al hacerlo le cambiamos el signo. Por eso  tenemos 2x - x.
2º el 17 le dejamos donde estaba y nos llevamos el 7 al segundo miembro (como era -7 se convierte en un + 7).

HALLAMOS EL PERÍMETRO y el ÁREA

 

1º- OBSERVA BIEN LAS FIGURAS: 
-    ¿de qué figuras se trata?: ninguna es  una figura de las que hemos visto en clase. Por tanto, lo `primero será descomponer esas  figuras en otras más pequeñas que sí conozcas (cuadrados, rectángulos, triángulos, trapecios, rombos, círculos).
-    Fíjate en la unidad que vienen los datos. En la figura a) vienen todos en mm   (milímetros). En la figura b) vienen mezclados, hay datos en cm (centímetros), en m(metros), dm (decímetros) y mm (milímetros).
En los dos casos será necesario pasar todas las unidades a la misma unidad y después operar con ella.  Por tanto habrá que recordar cómo pasar de una unidad a otra (medida de longitud)


¿QUÉ PIDE EL EJERCICIO?:  Te piden que halles el perímetro de cada figura.
La figura a) hay que expresarla en  decímetros (dm) y vemos que los datos vienen marcados en mm (milímetros). Podemos pasar todos los datos a dm y luego operar o primero podemos operar, obtener el resultado en mm y después pasarlo a dm, tal y como exige el  ejercicio.
En el ejercicio a) observamos tres figuras: un rectángulo, un cuadrado y un triángulo.   El perímetro es la suma de todos los lados. Comprueba si conoces todos los lados.  Lo más práctico es completar todos los datos que faltan:












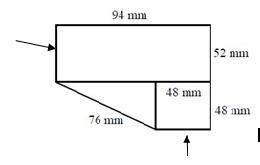
El perímetro sería, comenzando por arriba y hacia la  derecha:
94 + 52 + 48 + 48+ 76+  52 = 370 mm
Como nos piden en dm, la solución al ejercicio sería : 370mm= 3,70 dm


En la figura B optamos por  pasar todas las unidades que tiene la figura a la que nos piden, a metros. 

Por tanto la figura quedaría así:

Por tanto el Perímetros sería (comenzando por la línea superior y hacia la derecha):
0,134 + 0,062 + 0,062 + 0,06 + 0,03+ 0,06 + 0, 068 =  0,476 metros.

VAMOS A POR LAS ÁREAS

La primera figura se descompone en tres figuras conocidas:

Ahora aplicamos  las fórmulas de cada figura, para después sumarlas y hallar el área total.

ÁREA DEL RECTÁNGULO=  b . a =  94 . 52 =
ÁREA DEL TRIÁNGULO=  b. a   =  la base es 48 mm y la altura  94 menos 48 mm.
                                                  2
ÁREA DEL CUADRADO:  l . l =  48 . 48 =

La suma de todas las áreas dará como resultado el área total.

Figura 2:  Está formada por varias figuras: triángulos y  rectángulos.  Debes tener en cuenta que hay que operar en la misma unidad (utilizando por ejemplo los datos del ejercicio anterior).

Tenemos un tríangulo de color rojo. A= b.a   =
                                                                   2
Otros dos  triángulos  de color amarillo y gris , iguales. A= b.a =
                                                                                                 2
Un rectángulo verde.  A=  b. a=

Y un rectángulo pequeño, de color azul. A= b. a =

                                    ¿Cuál es la solución al ejercicio? ¿Qué área no podemos hallar porque nos faltan datos?  ¿Se pueden hallar los datos que faltan con lo que sabemos?

PERÍMETROS

Enlaces para repasar la teoría y  practicar lo visto en clase.

EL PERÍMETRO

PERÍMETROS

ÁREAS

PORCENTAJES Y PROPORCIONES

 

Para practicar... y aprender más

Navegando y navegando he encontrado una página muy interesante para practicar TODO  lo que estudiamos en clase de Matemáticas. Es la página de un colegio de Córdoba y de la editorial Santillana.
Si la visitais  (cosa que os recomiendo)  encontraréis muchos enlaces con ejercicios muy divertidos de cálculo mental, con varios niveles, de fracciones, números decimales  y de todos los temas estudiados en 6º de primaria.
Como ejemplo os dejo este sobre la prioridad de las operaciones y los paréntesis. Haz clic en la imagen y a jugar !!!!




ENLACE A LA PÁGINA